PythonでQuick Sortというアルゴリズムを使って数字の並び替えをしてみます。並び替える方法を他にもいろいろありますが、このQuick Sortはとても効率的に並び替えることができます。有名なアルゴリズムなのかもしれませんが、アルゴリズム初学者の自分には、非常に斬新に思えたので、まとめてみました。
なかなか、最初はややこしいので、理解するのに時間がかかりましたが、このアルゴリズムの考え方を使うといろいろな計算に応用ができます。しかも、パーツで分岐して並び替えをしていくので、計算量も大きくならないことが多いので、非常に効率的な計算をしてくれます。
Quick Sortの考え方
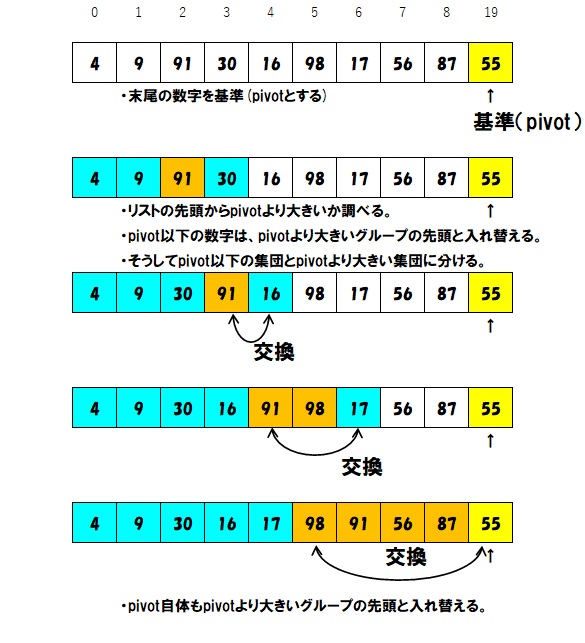
- 数字のリストで、一つの数字を基準(pivot)に決めます。
- リストの数字が、そのpivotより大きいか小さいかを考え、大きい数字のグループと、小さな数字のグループに分けます。
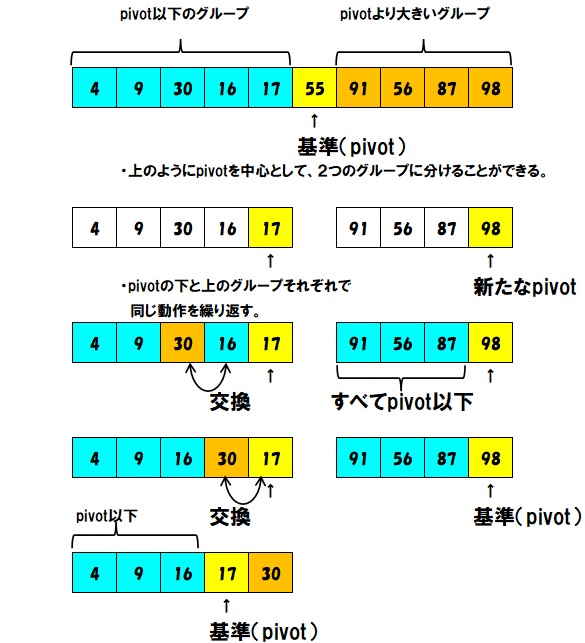
- さらにその大きなグループと小さなグループのそれぞれに対して、同じように一つの数字を基準(pivot)に決めて、さらにそのグループ内で、pivotより大きな数字のグループと小さな数字のグループに分けます。
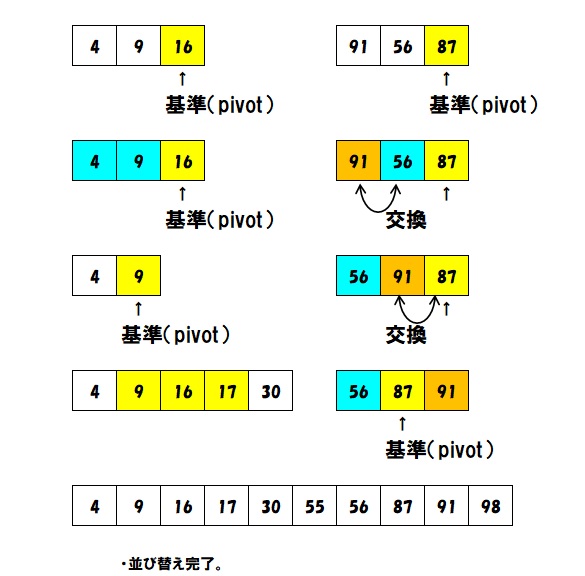
- 3を何度も繰り返し、それ以上分けらなくなるまで、分割していきます。
- 最後に分割した数字を一つに並べると、ソート完了です。
それを図で示すと下の通りです。ここでは10個の100以下の数字の並び変えをしています。
並び替えのポイントは、pivot以下のグループの末尾のインデックス番号を保持しておいて、pivot以下の数字が出てきたときに、その次のインデックスと入れ替えていくことで、効率的に2つのグループに分けることができます。
Pythonでのコードの書き方
コードは、「並び替えをする関数」と、「並び替えをする範囲を決める関数」の2つの関数からなります。「並び替えをする範囲を決める関数」は再帰関数を使うことによって、分けられなくなるまで、並び替えを実行し続けます。
それでは、まず、「並び替えをする関数」から書いていきます。ここでは、リスト全体、並び替える部分のインデックスの下限、インデックス上限の3つを引数として渡します。戻り値はpivotのインデックス番号とします。
続いて、再帰関数でpivotでの「並び替えをする範囲を決める関数」を書いていきます。ここでは、分けられなくなるまで再帰関数で上の「並び替えをする関数」を実行していきます。
ここでは、0から100のランダムな整数30個を並び替えます。
# pivotを中心に振り分ける
def pivot_rearrenge(numbers, low, high):
# 範囲の末尾をpivotに設定
pivot = numbers[high]
# pivot以下のグループの末尾のインデックス番号
# 開始時はlowの一つ下のインデックス番号をセット
j = low - 1
# lowからhighまでループを回す
for i in range(low, high+1):
if numbers[i] <= pivot:
# pivot以下のグループの末尾をずらす
j += 1
# numbers[i]をnumbers[j]と交換
numbers[j], numbers[i] = numbers[i], numbers[j]
# 最終的なpivotのインデックスを返す
return j
# pivotを設定する
def quick_sort(numbers):
# リスト本体とターゲットの下限、上限を渡す
def _pivot_set(numbers, low, high):
# lowとhighが同じ値になったら処理終了
if low < high:
# ターゲット内でpivotの設定
pivot_index = pivot_rearrenge(numbers, low, high)
# pivotより小さな部分を新たにターゲットにして実行
_pivot_set(numbers, low, pivot_index-1)
# pivotより大きな部分を新たにターゲットにして実行
_pivot_set(numbers, pivot_index+1, high)
# リストの全範囲をターゲットに設定
_pivot_set(numbers, 0, len(numbers)-1)
return numbers
import random
nums = [random.randint(0,100) for _ in range(30)]
print(nums)
print(quick_sort(nums))最後に
Quick Sortはリストの数字を細分化して、細かい単位で並び替えていくので、バラバラな並びの数列を効率的にソートしてくれます。再帰関数を使って、ターゲットを絞っていくアルゴリズムは、他でも応用できそうなので、今回は詳しく仕組みを勉強してみました。なかなかこの手のアルゴリズムは知っていないと書けないと思います。




コメント