Pythonでのビット演算の基礎まとめ

Python基礎

2022.09.292023.01.10

ビット演算子は個人的には普段ほとんど使うことはないのですが、知らないといざというときに使えません。今回はPythonでのビット演算と使いこなし方法を基礎からまとめてみました。

ビット演算子超基本シートシート（Python用）
２進数について
2進数の表記
ビット演算子
ビットシフト
ビット演算の使いこなしリンク

ビット演算子超基本シートシート（Python用）

PDFダウンロード

２進数について

２進数はゼロ(0)とイチ(1)だけで表される数字です。メモリへの書き込みや演算などは2進数でおこなっているそうですが、普段私などはあまり2進数を意識することはありません(;^_^A
今回はその2進数について勉強してまとめてみました。

下に10進数の1から15に相当する2進数を示しています。4桁の0と1の2進数では、0000を含めて、0～15までの16（=2⁴）種類の数を表現することができます。5桁であれば32(=2⁵)種類、8桁であれば256(=2⁸)種類の数を表すこと出来ます。

また、10進数では桁が増えると10倍ずつになっていきますが、2進数では桁が増えるごとに2倍ずつになっていきます。

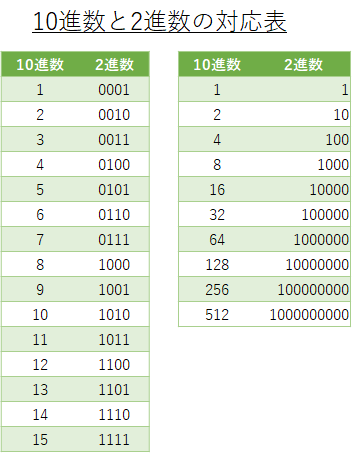
2進数の表記

数字を2進数で表示するには関数bin()を使います。また、2進数表示の数字は先頭に「0b」をつきます。変数に「z = 0b11110」のように2進数のまま代入することも出来ます。また、0と1のみからなる文字列は先頭に’0b’を付けて、int(‘0b1010’, 0)のように「int(接頭語付き2進数, 0)」と書くか、先頭に’0b’を付けずに、int(‘1010’, 2)のように「int(接頭語なし2進数, 2)」と書けば、整数型の数字に変換できます。

>>> x = 6
>>> y = 3
>>> bin(x)
'0b110'
>>> bin(y)
'0b11'
>>> z = 0b11110
>>> z
30
>>> int(s, 2)
10
>>> s = '1010'
>>> int('0b'+s, 0)
10
>>> int(s, 2)
10
>>>

型変換のオペレーション(2進数) 
（※8進数や16進数も接頭語や数字を変えれば同様の構文を適用可能）
2進数表示
bin(整数) → 0b+2進数で表示される
0b+2進数 → 2進数の数字として扱われる
format(整数, ‘b’) → 2進数の文字列として出力する
format(整数, ‘04b’) →4桁の2進数の文字列として出力する(0の後の数字が桁数)

2進数の文字列から整数へ変換
int(‘0b1011’, 0) → 2進数文字列(接頭語付き)から整数型に変換
Int(‘1011’, 2) → 2進数文字列(接頭語なし)から整数型に変換

ビット演算子

あらゆるビット演算は論理積(AND), 論理和(OR), 排他的論理和(XOR), 反転または否定(NOT)の4種類の演算子の組み合わせで記述することができます。それぞれの演算子の出力については下の表にまとめた通りです。

論理積(AND)・・・Pythonでは「&」で示す。A&Bで両方が1の時だけ1となり、それ以外は0
論理和(OR)・・・Pythonでは「|」で示す。A|Bでどちらかが1の時に1となり、両方が0の時だけ0
排他的論理和(XOR)・・・Pythonでは「^」で示す。A^Bでどちらか片方だけが1の時に1となり、両方1か両方0の時は0
反転、否定(NOT)・・・Pythonでは「~」で示す。1の時0で、0の時1で、反転させる。Pythonのビット演算で2進数を扱うときは符号付き２進数で考え、負の数を返すので、各桁を1で満たした2進数との理論積を取ることで、符号を消して反転のみを残すことができる。

>>> x = 6
>>> y = 3
>>> x & y
2  
>>> x | y
7   
>>> x ^ y
5   
>>> ~x
-7
>>> ~y
-4 
>>> format(x, '04b')
'0110'
>>> format(y, '04b')
'0011'
>>> format(x & y, '04b')
'0010'
>>> format(x | y, '04b')
'0111'
>>> format(x ^ y, '04b')
'0101'
>>> format(~x&0b1111, '04b')
'1001'
>>> format(~y&0b1111, '04b')
'1100'
>>>

ビットシフト

2進数の特徴的な処理にビットシフトがあります。下のように2進数の桁を増やしたり減らしたりする処理です。例えば、xという変数に対して、n桁分左へのシフトは「x<<n」と記述し、その処理によりxは2のn乗倍されます。一方で、n桁分右へのシフトは「x>>n」と書き、ｘは2のn乗で割った商（あまりは切り捨て）になります。それぞれ左と右へのシフトの様子を示すと下のようになります。それぞれ左にシフトした場合、増やした桁は0で埋められ、また、右のシフトにより桁はその分減ります。