トポロジカルソートについて徹底的に理解してみようと思います。トポロジカルソートは有向閉路を持たない有向グラフの最長経路を求めるのに使えるとあります。まず、有向閉路がよく分かりません。有向グラフとかの言葉も使い慣れないとよく分かりません。競技プログラミングAtCoder歴3カ月の初心者コーダーがかみ砕いて、説明してみました。言語はPythonを使います。
トポロジカルソートを使った例題
AtCoderの『DPまとめコンテスト』のG問題はトポロジカルソートを知っていると簡単に解けるそうそうです。
ちなみに、この手のグラフの問題は、王道の『全探索』を使っても解くことができます。ただし、全探索は時間が時間が掛かる場合があり、この問題は計算時間に2秒以内の制約がついており、筆者が深さ優先探索でトライしましたが、あえなくTLE(Time Limit Exceed; 時間切れ)で撃沈しています。(その時に書いたコード)
そこで、今回、トポロジカルソートを完全に理解して、この問題のクリアを狙っています。。。(実はこの記事を書き始めてた段階では解けていませんw)
グラフとは?有向グラフ、無向グラフとは?
ここでいうグラフはネットワークの繋がりの構造のことを表します。その中でその繋がりが矢印になっていて、一方通行のつながりのあるネットワークを「有向グラフ」、向きのないネットワークを「無向グラフ」と言うそうです。その時、つなぎ目のとる点のことをノードと言います。
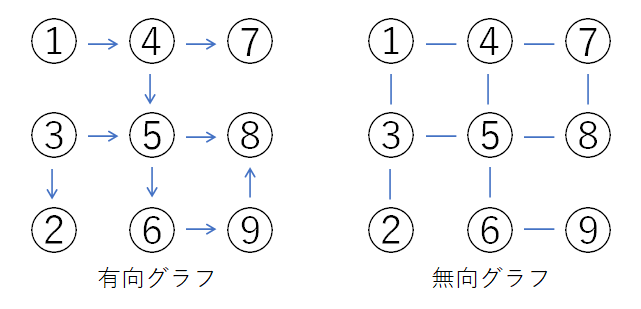
ここでは、有向グラフについて、掘り下げて考えたいと思います。
有向グラフをデータで表す
上の有向グラフをデータで表すとしたら、最も簡単な方法は、それぞれ矢印の始点と終点で数字で表すのが簡単です。例えば、上にあるグラフの左の有向グラフをリストで表すとしたら、下のようになります。
L = [[1,4], [4,7], [3,5], [5,8], [6,9], [4,5], [3,2], [5,6], [9,8]]この例では[始点, 終点]で各矢印の繋がりを表しています。
有向閉路とは?有向非巡回グラフ(DAG)とは?
閉路とは、道を進んでいったときに、元の点に戻ってしまうような循環しているネットワーク構造のことを言います。つまり、有向閉路とは矢印向きに進んでいくと、いつまでもグルグル回ってしまう部分のあるグラフのことを言います(循回グラフ)。そういった巡回する構造を持たない(矢印を進んいくとどこかで終点になる)ようなグラフを有向非巡回グラフ(英語で、Directed Acyclic Graph:DAG)と言います。
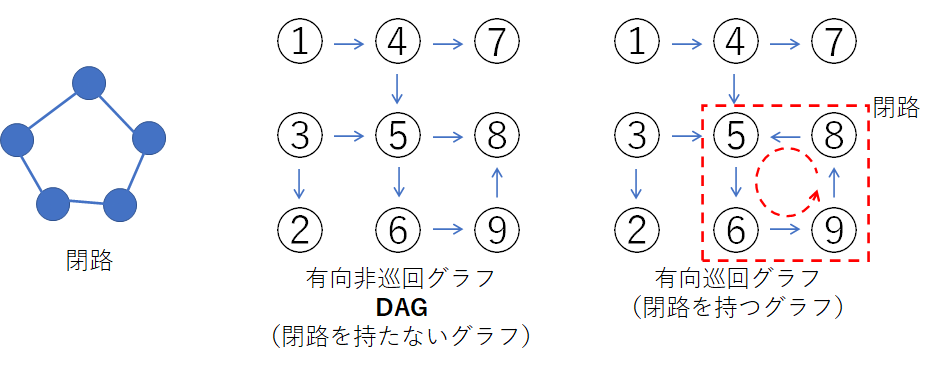
DAGは操作の手順や因果関係を表すのに便利なグラフです。
トポロジカルソートとは?
トポロジカルソートとはDAGの各点(ノード)の前後関係が分かるように順番をつけて並べる手法です。例えば、下のDAGの一番長い経路を並べて表すと下のように6つの点(ノード)を順番に並べることができます。
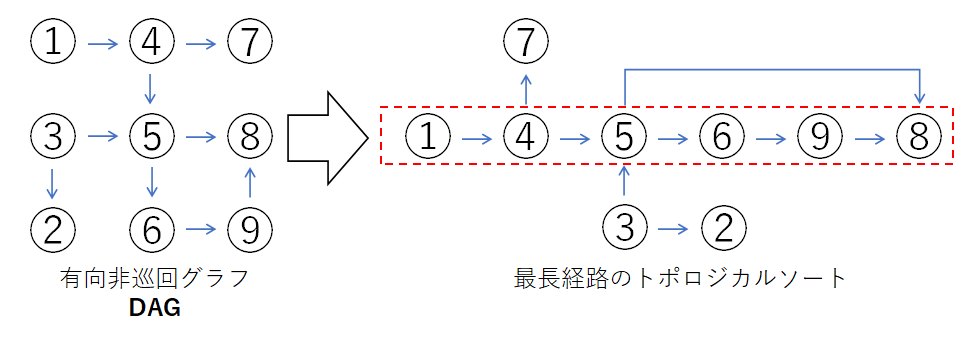
こういった短いネットワークであれば、見るだけで簡単に分かりますが、複雑ネットワークの経路をアルゴリズムで機械的なルールで簡単に、しかも効率的に並べるのはどうすればよいでしょう。実際にトポロジカルソートの手順をPythonで書いてみます。
トポロジカルソートの手順
入次数を考える
次数というのは、ある点(ノード)に結ばれているコネクションの数のことを言います。また、有向グラフの場合は入ってくるコネクションの数を入次数、出ていく数を出次数といいます。トポロジカルソートでは各ノードの入次数をカウントします。下の図では各ノードの入次数を調べています。
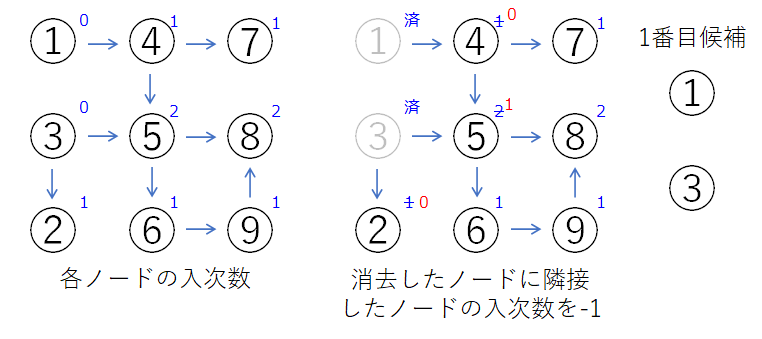
これを見ると、1と3が入次数が0であることが分かります。つまり入ってくるものがないので、もし順番でソートした時には最初の数となるノードであることが分かります。
入り数0のノードの隣接ノードを考える
次に2番目のノードを考えます。先ほどのノードに隣接しているノード(矢印が向いているノード)の入次数を-1します。その操作で入り次数が0になったノードは2番目の数となるノードだと分かります。この例では2と4が入次数が0になっています。そのうち、2から出ている矢印はないので、3→2の並びは2つで経路が終わっていることが分かります。4の方はまだ先があるので、再び、今度は残ったノードに隣接しているノードの入次数を-1します。
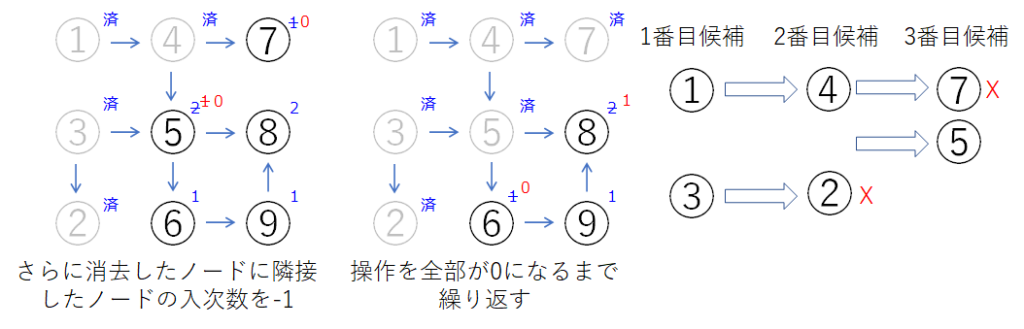
このような操作をすべてのノードが0になるまで繰り返したとき、最後まで残った数列が最長経路になります。
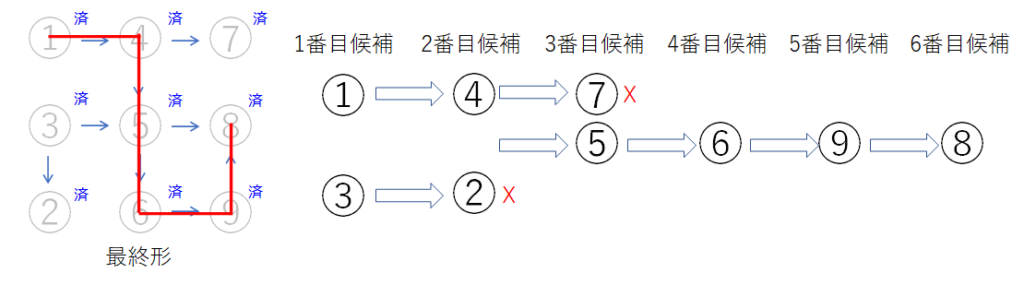
Pythonへの実装
それではこれをPythonに実装してみます。上の小さなグラフでは簡単すぎるので、AtCoderの『DPまとめコンテスト』のG問題へ回答する形でやってみます。グラフが大きくても、小さくても、どちらでも対応できると思いますので、そのあたりはあまり関係ありません。
from sys import stdin
input = stdin.readline
N, M = map(int, input().split())
G = [[] for _ in range(N)]
d = [0]*N
# グラフの出入のノードの番号を読み取り、各ノードの行先をGにリスト化
# 同時に入次数dをカウント
for i in range(M):
x, y = map(int, input().split())
G[x-1].append(y-1)
d[y-1] += 1
# 入次数が0のノードに隣接するノードをセットに追加
checklist = []
length = 0
for i in range(len(d)):
if d[i]==0:
checklist.append(i)
# 入次数が0のノードに隣接するノードの入次数を-1
# 入次数が0になったら次のノードリストに追加
# すべての入次数が0になるまで繰り返す
while len(checklist)>0:
nextlist = []
for i in checklist:
for j in G[i]:
d[j] -= 1
if d[j] == 0:
nextlist.append(j)
checklist = nextlist.copy()
length += 1
# 辺の数を出力
print(length-1)上のコードでACになるのを確認できました。全探索では実行時間2200ms以上掛かっていた計算が、10分の1以下の175msで実行できました。トポロジカルソートを使うと非常に効率的に計算できることが分かります。





コメント