Jupyter NotebookのMarkdownモードではTeX(テフ)を使って美しい数式を表示できます。今回はTeX記法で様々な統計の数式を書くことに挑戦してみました。
TeXとは
TeXは学術論文などできれいな整った文章を作成するのに用いられてきた文書作成言語です。私は化学系だったので、学生時代も使ったことはありませんでしたが、数式を多用する学科の知り合いはTeXを使って論文を書いていたと聞いています。最近もまだ使われているのかは、私は門外漢なので、よく知りません(;^_^A
一方で、Jupyter NotebookのMarkdownモードや、WordPressや一部のブログサイトの拡張機能を使って、TeX技法で数式を書くことができます。今回、Jupyter Notebookで様々な統計の数式を作成してみました。
Jupyter NotebookでTeX記法を使う
数式はJupyter NotebookのMarkdownセルで作成できます。マークダウンセルはノートブックのメニューからMarkdownを選択するか、セルを選んで、「m」キーを押すとそのセルがMarkdownセルに変換できます。Markdownセルでは、インラインで数式を挿入する方法と、別行立てで式を書く方法の2つの方法があります。
インラインで数式を書く方法
一次関数は$y=ax+b$の形で表されます。<br>
$y=ax+b$をxで積分すると、$\int ydx = \int (ax+b)dx = \dfrac{1}{2}ax^2+bx+C$となります。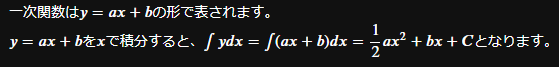
行間に$ [TeX記法] $のように、$の間に挟んで文中にTeXを配置すると、文章中に数式を表示ができます。文章の中に数式を入れ込みたいときはこちらを使うと良いでしょう。
別行立てで数式を書く方法
$$
x = \frac{-b\pm\sqrt{b^2-4ac}}{2a}
$$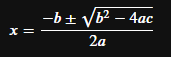
2つの$に挟んで記入することで別行立てで数式が表示できます。式だけで独立した行に記載したときはこちらを使うのが良いでしょう。
Jupyter Notebookで数式を記載するときの特徴
- Markdownモードではそもそも改行させるには、改行記号やダブルスペースなどを使う必要があります。数式を書く場合も改行したい場合は「\\」などの改行コードを入れる必要があります。
- \記号(Windowsの場合はバックスラッシュ記号)特殊文字として扱われ、\の後ろにコマンドを記載することにより、特殊文字や数式の形式を表現します。
- {}で囲むことにより、その中の文字列はひとかたまりの数式をして扱うことができます。また、{}の中にコマンドを書くことにより、レイアウト設定などの特殊な操作が可能です。
- 上付きと下付きの数字や記号はそれぞれ^と_続けて記載することで入力できます。文字の配置は各型に応じて、自動で整形してくれます。
TeX記法の記号や特殊文字
TeX記法の記号や特殊文字は下のリンク先のブログでまとめられています。ただし、Jupyter Notebookで全部が使えるわけでないので注意が必要です。ネットで「LaTeX」で検索すると、たくさんよいまとめページが見つかります。

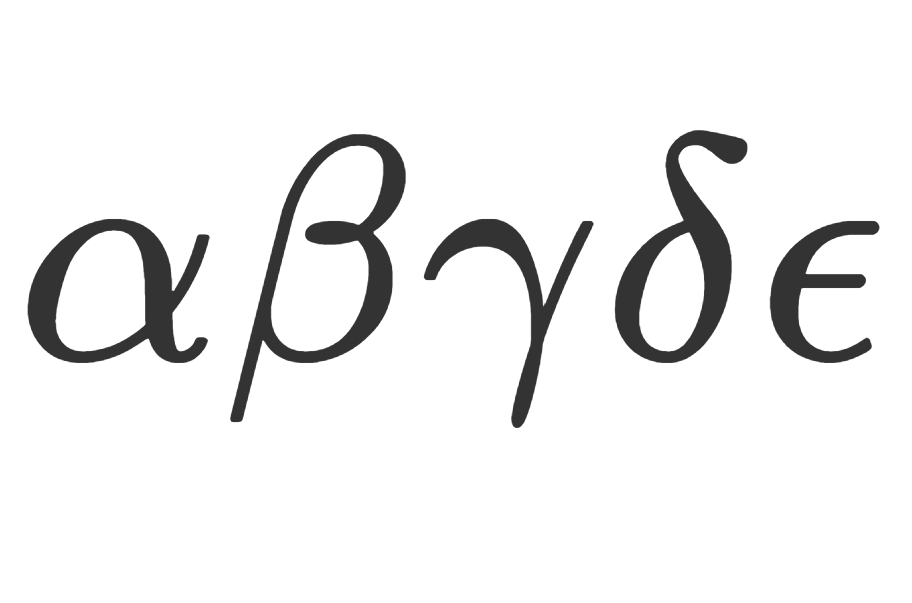
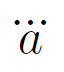
分数、ルート、シグマ、積分記号など
分数
分数は「\frac」で設定し、\frac{分子}{分母}で設定します。
$$
\frac{a+b}{c+d}
$$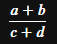
ルート
ルートは「\sqrt」で設定し、ルートの中身を{}の中に入れます。
$$
\sqrt{x^2+3x+2}
$$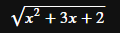
総和(シグマ)
シグマは「\sum」で設定し、シグマの上の表示するものは「^」の後に、下に表示するものは「_」の後に、それぞれ入力します。
$$
z = \sum^n_{k=1}n^2
$$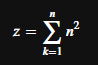
積分
積分記号は「\int」で設定し、積分記号の上の表示するものは「^」の後に、下に表示するものは「_」の後に、それぞれ入力します。
$$
F(x) = \int^{1}_{-1}(3x^2+2)dx
$$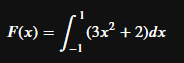
レイアウトを設定する
各種レイアウトの設定に詳しくは下のリンク先ブログを参照してください。ここでは、「\\」での改行と、「align」の行揃えの実例を見ます。
改行
$$
x^2-4x+4 \\
x^3-1
$$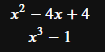
ここで、もし、「\\」の改行コードを入れない場合、2つの式は横に繋がります。
複数行の式の行揃え
「align」を使うと、複数行の数式の「=」の位置を揃えたり、教科書みたいなレイアウトにできます。alignは開始点と終点にそれぞれ「\begin{align}」「\end{align}」をおいて、その記号に挟まれた間の式が有効になります。奇数個目の「&」の位置が縦にそろいます。偶数個目の「&」はスペースを入れてくれます。
$$
\begin{align}
y &= (x-1)^3 \\
&= (x^2-2x+1)(x-1) \\
&= x^3-3x^2+3x-1 &&(1.1)\\
\\
y+1&=x^3-3x^2+3x-1+1 \\
&=x^3-3x^2+3x &&(1.2)
\end{align}
$$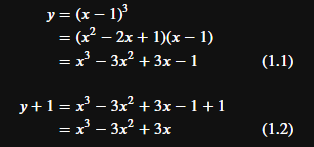
統計の数式を書いてみる
ここからは上記の様々なルールを組み合わせて式を作成します。分からない記号はgoogle先生に「LaTex + 分からない記号」を入れると大抵コード例を示してくれます。書きながら、確認していけば、難しくなかったです。慣れるとスラスラと式が書けるようになるので、見た目ほどややこしくはないです。
各種統計の数式のMarkdown記述
$$
\begin{align}
&\textrm{標本平均(Sample Mean)}\\
&&\bar{x}&=\frac{x_1+\dots+x_n}{n}=\frac{1}{n}\sum_{k=1}^n x_k \quad\quad &&(1.1) \\
\\
&\textrm{中央値(Median)}\\
&&\tilde{x}&=\begin{cases}
x_{m} \quad (n=2m-1) \\
\dfrac{x_{m}+x_{m+1}}{2}\quad (n=2m) \\
\end{cases}\quad (m\geqq 1は自然数) \quad\quad &&(1.2) \\
\\
&\textrm{標本分散(Sample Variance)}\\
&&s^2_x&=\frac{1}{n}\sum_{i=1}^n (x_i -\bar{x})^2 \quad\quad &&(1.3) \\
\\
&\textrm{標本標準偏差(Sample Standard Deviation)}\\
&&s_x&=\sqrt{s^2_x}=\sqrt{\frac{1}{n}\sum_{i=1}^{n} (x_i-\bar{x})^2} \quad\quad &&(1.4) \\
\\
&\textrm{標本共分散(Sample Covariance)}\\
&&s_{xy}&=\frac{1}{n}\sum_{i=1}^{n} (x_i-\bar{x})(y_i-\bar{y})=\frac{1}{n}\sum_{i=1}^{n}x_{i}y_{i}-\bar{x}\cdot\bar{y}\quad\quad &&(1.5) \\
\\
&\textrm{標本相関係数(Sample Correlation Coefficient)}\\
&&r_{xy}&=\frac{s_{xy}}{\sqrt{s^2_x s^2_y}}\quad\quad&&(1.6) \\
\end{align}
$$表示される数式

参考リンク
すごく丁寧にTeX記法がまとめられていて、参考となるテクニックがいっぱいです。


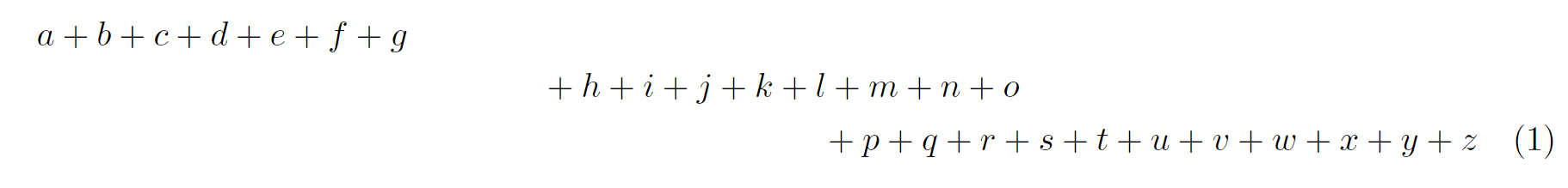



コメント