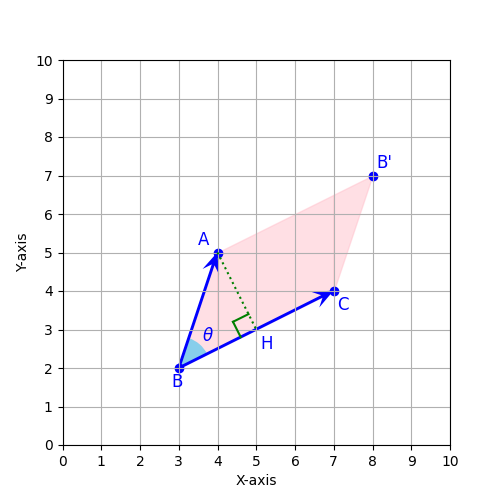
matplotlibを使うと慣れれば複雑な図も簡単に作ることができます。今回は様々な要素を組み合わせて、XY平面にベクトルなどの様々な要素を組み合わせた図を作ってみました。最終的な完成図は下のような感じです。ベクトルや角度、平行四辺形の領域の塗りつぶし、ギリシア文字の使用など、様々な要素をキャンパスに設置して、考えた通りの構成の図を作ることができます。
matplotlibのインポート
matplotlibをインストールしていない場合は、pipコマンドなどでインストールを行っておきます。matplotlibを使うために、最初に下記のようにインポートをします。また、ここでは座標を記述するためにNumpyを使いますので、Numpyもインポートします。
import matplotlib.pyplot as plt
from matplotlib import patches
import numpy as npmatplotlibのプロットエリアに方眼紙を作る
最初にmatplotlibのプロットエリアに方眼紙を作成します。ここでは10 x 10のXY平面の方眼紙を準備します。プロットする範囲や目盛ラベルの設定など、任意に設定できます。この時、X軸とY軸の比率を同じにしておくと正方形のマス目の方眼紙を作ることができます。
import matplotlib.pyplot as plt
# matplotlibのスタイルを設定(デフォルト)
plt.style.use('default')
# 図のサイズを設定
fig, ax = plt.subplots(figsize=(5, 5))
# グリッド線を追加
ax.grid()
# 目盛ラベルを設定
ax.set_xticks(np.arange(0,11,1))
ax.set_yticks(np.arange(0,11,1))
# 軸の表示範囲を設定
ax.set_xlim(0,10)
ax.set_ylim(0,10)
# 軸ラベルを設定
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# ここにプロットする図を設定
# 図を表示
plt.show()
様々な要素の追加
それでは、図形を配置するキャンパスの準備できましたので、様々な要素を追加していきます。基本的にはsubplotsで設定した図形の本体のインスタンスであるaxに様々な要素を追加していくだけになりますので、お絵かき感覚で好きなものを入れられます。
点A、点B、点C、点B’の追加
点はscatterで追加できます。引数にはx座標とy座標を入力します。下にはそれぞれの点を設定する場合と、複数の点をリストでまとめる場合の2種類の表記方法で書いています。同じ種類の点を打ちたい場合はまとめてしまった方がシンプルです。
matplotlib.axes.Axes.scatter(公式ドキュメント)
# 図中に点を入力する
ax.scatter(4,5, color='blue')
ax.scatter(3,2, color='blue')
ax.scatter(7,4, color='blue')
ax.scatter(8,7, color='blue')まとめて入力する場合
# 図中に点を入力する
ax.scatter([4, 3, 7, 8],[5, 2, 4, 7], color='blue')また、図中にはテキストを入れることができます。ここでは、点A、点B、点C、点B’を表すアルファベットを入力します。示している点の近くに来るようにX座標とY座標を調節して見やすいように配置します。一様に点との位置関係を決めるより、手動で調節しながらの方がうまくいきます。まとめたい場合はFor文などのループで引数を渡してやるといいかもしれません。
# 図中にテキストを入力する
ax.text(3.5,5.2,"A", fontsize='large',color='blue')
ax.text(2.8,1.5,"B", fontsize='large',color='blue')
ax.text(7.1,3.5,"C", fontsize='large',color='blue')
ax.text(8.1,7.2,"B'", fontsize='large',color='blue')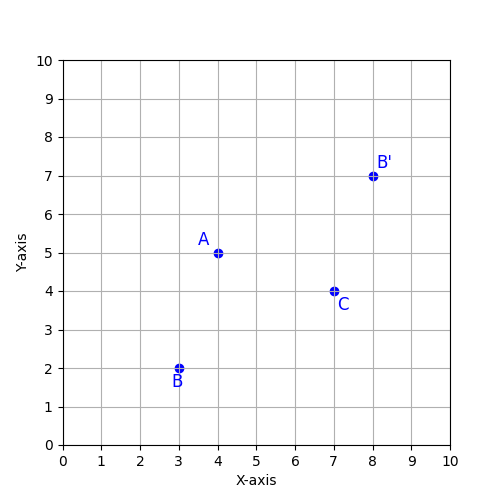
ベクトルの追加
ベクトルはquiverを使って描画します。ベクトルの始点(x, y)、ベクトルの向き(x, y)を最初に引数で指定します。scale_unitsは’xy’、scaleは1を指定することで、マス目と等倍の大きさでベクトルを描画できます。headlengthとheadwidthを調整して、矢印の形を好きなように変えることができます。なお、ベクトルについてはpyplot.arrowを使っても、表すことができるようですので、お好きな方をお使いいただけます。
matplotlib.quiver.Quiver(公式ドキュメント)
# 図中にベクトルを描く
plt.quiver(3, 2, 4, 2, scale_units='xy', scale=1, color='blue', headlength = 7, headwidth=6)
plt.quiver(3, 2, 1, 3, scale_units='xy', scale=1, color='blue', headlength = 7, headwidth=6)複数のベクトルをリストでまとめて記述することもできます。
# 図中にベクトルを描く
plt.quiver([3,3], [2,2], [4,1], [2,3], scale_units='xy', scale=1, color='blue',
headlength = 7, headwidth=6)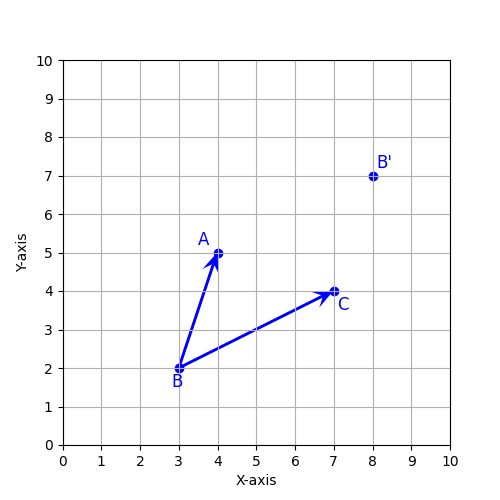
線分を追加
線分はmatplotlibの折れ線グラフでおなじみのplotで記述できます。plotは指定する複数の点を結ぶことができます。各頂点のX座標とY座標をそれぞれリストで引数に渡します。2点を結ぶ線分の場合は、[X1, X2], [Y1, Y2]を引数に記述します。ここでは、点AからベクトルBCと垂直に交わる線分AHを点線で記述します。直角の描画は、座標を計算し、(4.6, 2.8), (4.4, 3.2), (4.8, 3.4)の3点を結ぶ直線として設定しました。
ここでは、垂線の交わる点にHを追加しています。
matplotlib.pyplot.plot(公式ドキュメント)
# 図中に線分を描く
ax.plot([4,5],[5,3], ':', color = 'green')
ax.text(5.1,2.5,"H", fontsize='large',color='blue')
# 図中に直角を描く
ax.plot([4.6, 4.4, 4.8],[2.8, 3.2, 3.4], color = 'green')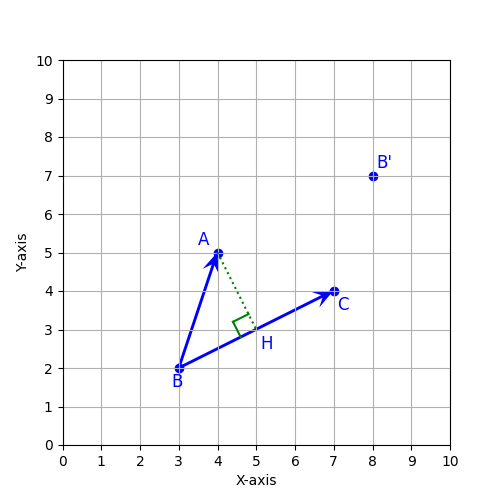
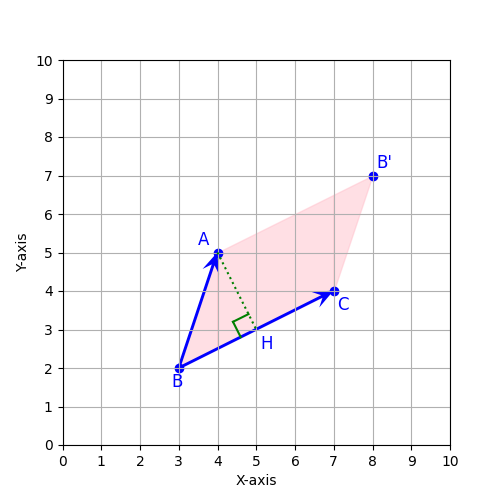
領域を塗りつぶす
図の2つの線に挟まれた部分を塗りつぶすことできます。ここでは、「fill_between」を使って、平行四辺形ABCB’を塗りつぶしてみます。塗りつぶす領域をX = 3~4、4~7、7~8の3つの領域に分けて順番に考えます。
X = 3~4の区間 ⇒BCとABの挟まれた部分を塗りつぶす
X = 4~7の区間 ⇒BCとAB’で挟まれた部分を塗りつぶす
X = 7~8の区間 ⇒CB’とAB’で挟まれた部分を塗りつぶす
fill_betweenでは指定したXの区間に対して、Y1とY2の間を指定した色で塗りつぶてくれます。
matplotlib.axes.Axes.fill_between(公式ドキュメント)
# 領域を塗りつぶす
ax.fill_between([3, 4, 7, 8], [2, 2.5, 4 ,7], [2, 5, 6.5, 7], color='pink', alpha=0.5)ここでは、塗りつぶす操作をベクトルなどを描いた後に行うと、ベクトルの一部が薄くなってしまうので、この操作は上の諸々の操作の前に持ってきています。(ページの最後のコード全体を参照)
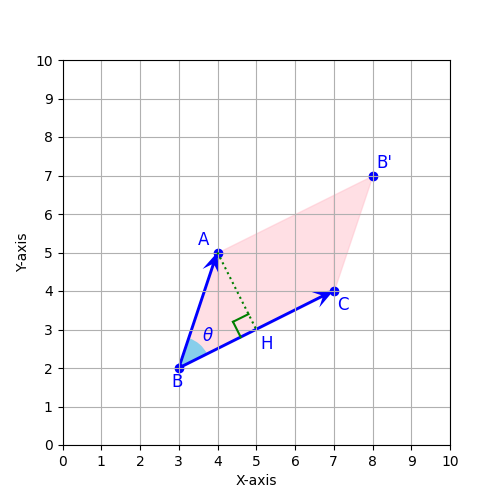
角ABCの角度θの表示
角ABCに角度θの表示を扇形で設定します。matplotlibには円や扇形、多角形などの様々な図形を「matplotlib.patches」で描くことができます。扇形はWedgeのクラスを使用します。Wedgeのクラスに中心座標、半径、開始角、終了角などの扇形の情報を渡して、インスタンスを作成し、それをadd_patchであてがうことで扇形を表示できます。
matplotlib.patches(公式ドキュメント)
matplotlib.patches.Wedge(公式ドキュメント)
ここでは、中心座標(3, 2)に半径0.8の扇形を描画します。ただし、開始角、終了角は計算で求める必要があります。ここでは、numpy.arctanの関数を使って、開始角と終了角を計算しています。matplotlibの角度は、時計の3時の方向が0度で、そこから反時計周りに角度をカウントします。扇形の開始角はちょうどBCの傾きで、終了角はABの傾きで、それぞれ、1/2と3です。傾きの角度はnumpyのarctanの関数でラジアン単位で求めることができますので、それを円周率で割って、180を掛けることで、度数表記の角度を求めることができます。
角度の部分には「θ」を表示します。matplotlibはTeXマークアップでの数式等の表記が可能です。matplotlibで「θ」を表示するために、TeXで表記し、テキストで出力します。TeXマークアップではギリシア文字以外に、様々な複雑な数式を表現することができます。
Writing mathematical expressions(公式ドキュメント)
# 図中に角度を描く
wedge = patches.Wedge((3,2) ,0.8 ,theta1=np.arctan(1/2)/np.pi*180, theta2 = np.arctan(3)/np.pi*180,
color="skyblue", label="Wedge")
ax.add_patch(wedge)
# θを表示する
ax.text(3.6,2.7, r'$\theta$', fontsize='large',color='blue')これで完成です。
完成したコード全体
最後にコード全体を示します。matplotlibのバージョン等によってはうまく思ったような表示ができないかもしれませんが、詳しい使い方は公式ドキュメントの説明を参照いただけたらと思います。キャンパスに部品を次々に配置していく感覚で試しながら作っていけます。matplotlibは他にも膨大な図形のパーツがあるので、都度、いろいろなことを試しながらやっていくと楽しいと思います。
どんな図形が書けるのかと興味がある方は、公式ホームページのギャラリーやチートシートをご参照ください。
matplotlib gallery(公式ドキュメント)
Matplotlib cheatsheets and handouts(公式ドキュメント)
import matplotlib.pyplot as plt
from matplotlib import patches
import numpy as np
# matplotlibのスタイルを設定(デフォルト)
plt.style.use('default')
# 図のサイズを設定
fig, ax = plt.subplots(figsize=(5, 5))
# グリッド線を追加
ax.grid()
# 目盛ラベルを設定
ax.set_xticks(np.arange(0,11,1))
ax.set_yticks(np.arange(0,11,1))
# 軸の表示範囲を設定
ax.set_xlim(0,10)
ax.set_ylim(0,10)
# 軸ラベルを設定
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
# ここにプロットする図を設定
# 領域を塗りつぶす
ax.fill_between([3, 4, 7, 8], [2, 2.5, 4 ,7], [2, 5, 6.5, 7], color='pink', alpha=0.5)
# 図中に角度を描く
wedge = patches.Wedge((3,2) ,0.8 ,theta1=np.arctan(1/2)/np.pi*180, theta2 = np.arctan(3)/np.pi*180,
color="skyblue", label="Wedge")
ax.add_patch(wedge)
# 図中にテキストを入力する
ax.text(3.5,5.2,"A", fontsize='large',color='blue')
ax.text(2.8,1.5,"B", fontsize='large',color='blue')
ax.text(7.1,3.5,"C", fontsize='large',color='blue')
ax.text(8.1,7.2,"B'", fontsize='large',color='blue')
ax.text(5.1,2.5,"H", fontsize='large',color='blue')
# θを表示する
ax.text(3.6,2.7, r'$\theta$', fontsize='large',color='blue')
# 図中に点を入力する
ax.scatter([4, 3, 7, 8],[5, 2, 4, 7], color='blue')
# 図中にベクトルを描く
plt.quiver([3,3], [2,2], [4,1], [2,3], scale_units='xy', scale=1, color='blue',
headlength = 7, headwidth=6)
# 図中に線分を描く
ax.plot([4,5],[5,3], ':', color = 'green')
# 図中に直角を描く
ax.plot([4.6, 4.4, 4.8],[2.8, 3.2, 3.4], color = 'green')
# 図を表示
plt.show()
完成図
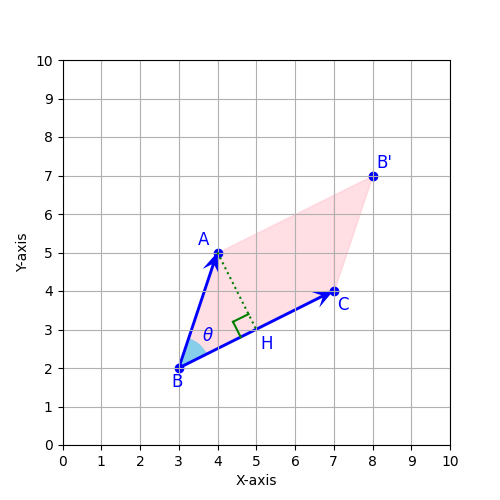
終わりに
matplotlibを使って、少し複雑なグラフの表記に挑戦しました。matplotlibはすべてを把握するのが難しいほど多様なことができます。今回、その中の機能の一部を実装してみました。使い方次第では、かなり高度な図形を描くことができそうです。




コメント